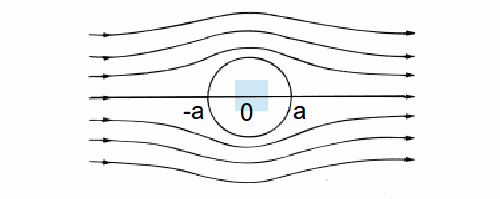
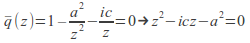We can model the flow of a fluid past a circular cylinder of constant cross section and radius![]() with the model flow velocity function
with the model flow velocity function![]() When
When![]()
![]() are called stagnation points.
are called stagnation points.
The complex velocity potential is given by![]() (1)
(1)
The boundary of the cylinder consists of streamlines, since fluid cannot enter or exit from the surface of the cylinder. There are other possible flows for which the surface of the cylinder is made up of streamlines. The complex velocity potential function![]() (2) where setc-{^pi} is the complex plane with the non positive real axis deleted.
(2) where setc-{^pi} is the complex plane with the non positive real axis deleted.
corresponds to vortex flow with streamlines consisting of circles of centre 0.
We can add the velocity potential functions to obtain a new velocity potential function
![]()
The conjugate velocity function is![]() so the model flow velocity function is
so the model flow velocity function is![]() (3)
(3)
The model flow velocity function has the following properties:
-
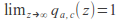
-
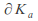 (the boundary of the cylinder) consists of streamlines for
(the boundary of the cylinder) consists of streamlines for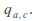
-
For any simple closed contour
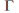 surrounding
surrounding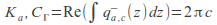 (we call
(we call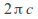 the circulation around
the circulation around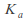 ) and
) and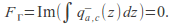
-
The stagnation points of the flow (3) are the solutions to