If![]() is a Mobius transformation, then the domain is
is a Mobius transformation, then the domain is![]() since if
since if![]() the denominator is zero. If
the denominator is zero. If![]() then the domain is
then the domain is![]()
We can extend Mobius transformations to the whole of![]() including the point at infinity by introducing the extended complex plane
including the point at infinity by introducing the extended complex plane![]()
We define the extended Mobius transformation![]() by
by
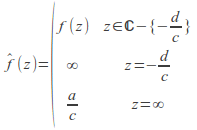
We can define the extended Mobius transformation![]() by
by
![]()
We can test for the group properties – identity, closure, inverse and associativity – one by one.
-
The identity is an extended Mobius transformation with a=1 and b=c=d=0 . Note that the identity sends the point at infinity to the point at infinity .
-
If
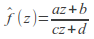 and
and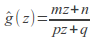 then
then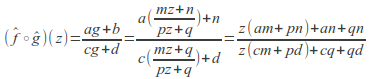 which is a Mobius transformation so the closure axiom is satisfied.
which is a Mobius transformation so the closure axiom is satisfied. -
If
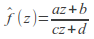 then
then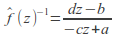 so the inverse axiom is satisfied.
so the inverse axiom is satisfied. -
Associativity follows from the general property of composition of functions.
All the group axioms are satisfied so the set of extended Mobius transformations is a group.