The nature of periodic points – such that![]() for some
for some![]() so that repeated applications of
so that repeated applications of![]() eventually return the value
eventually return the value![]() - for
- for![]()
![]() depends on whether the point is an interior or boundary point of the keep set
depends on whether the point is an interior or boundary point of the keep set![]() of
of![]()
If![]() is attracting then
is attracting then![]() is an interior point of
is an interior point of![]()
If![]() is repelling then
is repelling then![]() is a boundary point of
is a boundary point of![]()
Proof
Suppose that![]() is an attracting periodic point of
is an attracting periodic point of![]() with period
with period![]() Then
Then![]() is an attracting fixed point of
is an attracting fixed point of![]() hence there is an open disc with centre
hence there is an open disc with centre![]() whose points are attracted to
whose points are attracted to![]() under repeated applications of
under repeated applications of![]() These points do not escape to infinity under iteration by
These points do not escape to infinity under iteration by![]() so lie in
so lie in![]() and
and![]() is an interior fixed point of
is an interior fixed point of![]()
Next suppose that![]() is a repelling fixed point so that
is a repelling fixed point so that![]() and
and![]()
Since![]() we must show that
we must show that![]() is not an interior point of
is not an interior point of![]() If it were an interior point then we could choose an open disc
If it were an interior point then we could choose an open disc![]() lying in
lying in![]() so that
so that![]() for
for![]() and
and![]()
and![]() for
for![]() and
and![]() (1)
(1)
Now apply Cauchy's Estimate to each polynomial![]() to deduce that
to deduce that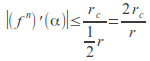 for
for ![]()
By the Chain Rule![]()
since![]() is a fixed point of
is a fixed point of![]()
![]() so the sequences
so the sequences![]()
![]() tend to infinity, contrary to (1) so
tend to infinity, contrary to (1) so![]()
A similar argument applies if![]() is a repelling periodic point of
is a repelling periodic point of![]() with period
with period![]()