Julia Sets
The Julia set of a quadratic function![]() is the boundary of the keep set
is the boundary of the keep set![]() or the boundary of the escape set
or the boundary of the escape set![]() and separates the points which escape to infinity under repeated iteration by
and separates the points which escape to infinity under repeated iteration by![]() and those which don't. The Julia set contains all the periodic repelling points of
and those which don't. The Julia set contains all the periodic repelling points of![]() and is the smallest closed set which contains all the repelling periodic periodic points of f. Two are illustrated below.
and is the smallest closed set which contains all the repelling periodic periodic points of f. Two are illustrated below.

The Julia set has the following properties:
For each
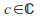 the Julia set
the Julia set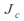 is a non empty compact subset of
is a non empty compact subset of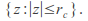
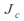 is completely invariant.
is completely invariant.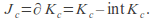
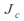 is symmetric under rotation by
is symmetric under rotation by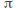 about 0.
about 0.
The Julia set is often plotted using the following method. If![]() then the solutions of
then the solutions of![]() also lie in
also lie in![]() The solution are
The solution are![]() so backwards iteration gives two new points of
so backwards iteration gives two new points of![]()
![]() and
and![]() iterating backwards again with these two points gives four new points
iterating backwards again with these two points gives four new points![]() and
and![]() Iterating backwards repeatedly gives more points. It can be shown that the Julia set is the smallest closed set containing all the backwards iterates of any given point of
Iterating backwards repeatedly gives more points. It can be shown that the Julia set is the smallest closed set containing all the backwards iterates of any given point of![]() Because of the amount of calculation involved, not all the backwards iterates are calculated at each stage. A single iterate from each stage may be randomly selected at the backwards iterates found for that point.
Because of the amount of calculation involved, not all the backwards iterates are calculated at each stage. A single iterate from each stage may be randomly selected at the backwards iterates found for that point.