Theorem
Let
be a function with domain
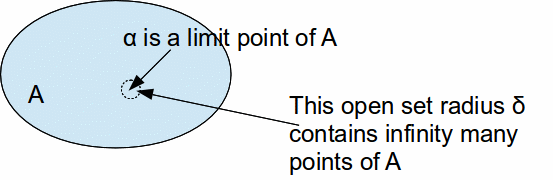
and suppose that
is a limit point of
so that every open neighbourhood of
contains infinitely many points of
the following statements are equivalent:
-
f is continuous at
-
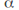
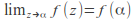
Proof
Suppose thatis continuous at
If
is any sequence in
with
then it follows that for
we can find
such that
implies
Hence
Conversely suppose that
If is any sequence inwithand
is the subsequence ofconsisting of those terms different from
then
since
and
The remaining subsequenceofsatisfies
for all
so
soandis continuous at