A Mobius transformation is any rational function of the form
where
and
satisfy
Properties:
Every Mobius transformation is conformal – preserves angles – and analytic on
Every Mobius transformation is either a linear function or a quotient of linear functions. If
then
and
Every Mobius transformation
may be extended to
so that ifthen
and
The extended function is labelled
Extended Mobius transformations map
one to one onto
and generalized circles – circles and lines – onto generalized circles.
Ifthen
where
The set of extended Mobius transformations has the following group properties:
-
Closure: If
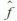and
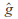are extended Mobius transformations then so is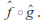
-
Identity: The identity function in
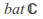is an extended Mobius transformation. -
Associativity: If
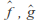and
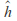are extended Mobius transformations then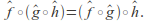
An extended Mobius transformation
has at least one fixed point
such that
An extended Mobius transformation is defined by it's effect on three distinct points.
Given three distinct points
inand any other three distinct points
in 
there is a unique extended Mobius transformation that sends
to
to
to 
In particular ifare
respectively then
If
are generalized circles then there is an extended Mobius transformation that maps
to