For each![]() the escape set
the escape set![]() and the keep set
and the keep set![]() of the basic quadratic function
of the basic quadratic function![]() have the following properties
have the following properties
-
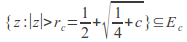 and
and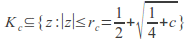
-
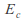 is open and
is open and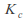 is close
is close -
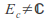 and
and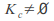
-
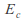 and
and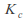 are both invariant under
are both invariant under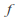
-
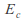 and
and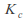 are both symmetric under rotation by
are both symmetric under rotation by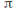 about 0.
about 0. -
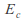 is connected and
is connected and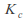 has no holes in it
has no holes in it
Proof
a) By the backwards form of the triangle inequality![]() (1)
(1)
![]() is the positive solution of the quadratic equation
is the positive solution of the quadratic equation![]() We claim that if
We claim that if![]() then
then![]() (2) for
(2) for![]()
Indeed if![]() then
then![]()
as required by (2). (1) and (2) now give![]() for
for![]()
If![]() then we can apply this inequality successively to
then we can apply this inequality successively to![]() to deduce that
to deduce that![]() is increasing and
is increasing and![]() as
as![]()
b) Suppose![]() then
then![]() as
as![]() so for some
so for some![]() Let
Let ![]() Since
Since![]() and
and![]() is a polynomial
is a polynomial![]() is continuous at
is continuous at![]() so there exists
so there exists![]() such that
such that![]() implies
implies![]() hence
hence![]() It follows that
It follows that![]() implies
implies![]() as
as![]() so that
so that![]() and
and![]() is open.
is open.
c) The set![]() is not the whole of
is not the whole of![]() because it does not include the fixed points of
because it does not include the fixed points of![]()
d)![]() as
as![]()
![]() as
as![]()
![]() as
as![]()
![]()
e) Since the set![]() is connected and
is connected and![]() it is sufficient to show that each point
it is sufficient to show that each point![]() can be joined to some point of
can be joined to some point of![]() by a path in
by a path in![]() The proof is by contradiction.
The proof is by contradiction.
Suppose that![]() cannot be joined to
cannot be joined to![]() Define
Define ![]() then
then![]() since
since![]()
![]() is open because if
is open because if![]() can be joined to
can be joined to![]() then so can points of any open disc in
then so can points of any open disc in![]() with centre
with centre![]() and
and![]() is connected because pairs of points in
is connected because pairs of points in![]() can be joined in
can be joined in![]() via
via![]() R is thus a subset of
R is thus a subset of![]() Since
Since![]() cannot be joined in
cannot be joined in![]() to
to![]() and
and![]() is open we deduce
is open we deduce![]()
Now use the maximum principle. If![]() then
then![]() else we increase the size of
else we increase the size of![]() so
so![]() for
for![]()
Applying the maximum principle to each polynomial function![]() on
on![]() we obtain
we obtain![]() for
for![]() and
and![]() which contradicts that
which contradicts that![]() hence
hence![]() is connected.
is connected.