Proving the Differentiation Under the Integral Sign Formula

• Print

Theorem

Letbe a region and letbe a complex valued function of two variablesandsuch that

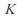1. is analytic in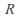as a function of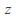for each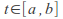

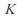2. and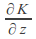are continuous on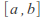as functions of t for each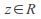

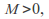
3. For some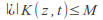for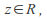

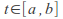
Then the functionwithis analytic onandfor(1)

Proof: Letand choose a circleinwith centreand radiussuch that the inside oflies entirely inIflies insidethen we have by assumption 1 and Cauchy's Integral Formula,

and

and by Cauchy's First Derivative Formula,for each

Hence, if f is given by (1) then

say. We need to show thatas

henceas