Suppose that a complex valued function![]() operating on complex numbers has a singularity at
operating on complex numbers has a singularity at![]() Then
Then
-
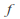 has a removable singularity at
has a removable singularity at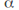 if there is a function
if there is a function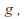 analytic at
analytic at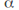 such that
such that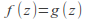 for
for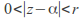
-
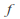 has a pole of order
has a pole of order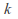 at
at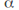 if there is a function
if there is a function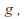 analytic at
analytic at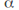 with
with 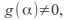 and a positive number
and a positive number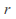 such that
such that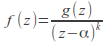 for
for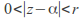
-
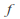 has an essential singularity at
has an essential singularity at if the singularity at
if the singularity at is neither removable or a pole.
is neither removable or a pole.
Example:![]() has a singularity at 0 since the denominator =0 at
has a singularity at 0 since the denominator =0 at![]() but the singularity is removable since
but the singularity is removable since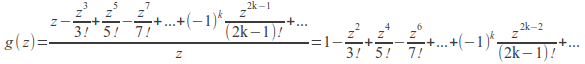
is analytic at![]() and
and![]() on
on![]()
Example:![]()
![]() has two poles, one at
has two poles, one at![]() and one at
and one at![]()
![]() so the pole at
so the pole at![]() has order 1.
has order 1.
![]() so the pole at
so the pole at![]() has order 2
has order 2
Example:![]() has an essential singularity at
has an essential singularity at![]() To see this, write
To see this, write![]()
Because the powers of![]() are negative and becoming larger without limit, the singularity is essential. We cannot multiply
are negative and becoming larger without limit, the singularity is essential. We cannot multiply![]() by
by![]() for any
for any![]() to make
to make![]() analytic.
analytic.