A function f defined on a region R has a local maximum at a point %alpha in R if there is some r >0 such that![]() and
and![]() for
for![]()
For example,![]() then f has a local maximum at
then f has a local maximum at![]() On the other hand
On the other hand![]() has no local maximum at all.
has no local maximum at all.
Suppose that![]() is a non – constant analytic function with domain a region
is a non – constant analytic function with domain a region![]() and that
and that![]() If
If![]() has a local maximum at
has a local maximum at![]() then there is some
then there is some![]() such that
such that
![]() for
for![]() (1)
(1)
But if![]() then
then![]() is an open set containing
is an open set containing![]() by the Open Mapping Theorem. and so
by the Open Mapping Theorem. and so![]() contains an open disc,
contains an open disc,![]() say, centred at
say, centred at![]()
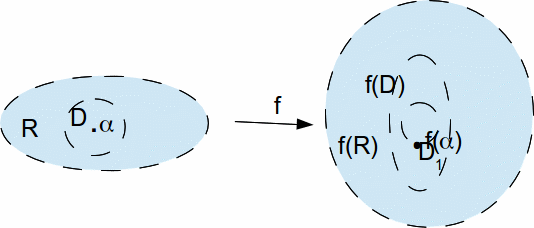
We can show that there is some point![]() such that
such that![]()
If![]() then this is evident because
then this is evident because![]() is non – constant. If
is non – constant. If![]() then a
then a![]() can be found by extending the line segment from 0 to
can be found by extending the line segment from 0 to![]()
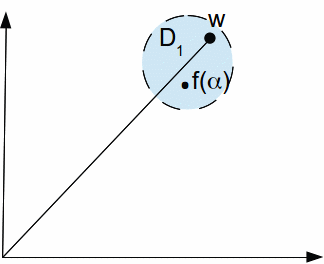
Since![]() we have
we have![]() for some
for some![]() and hence
and hence![]() contradicting (1). The following result is proved.
contradicting (1). The following result is proved.
The Local Maximum Principle
Let a function![]() be analytic on a region
be analytic on a region![]() If
If![]() is non – constant on
is non – constant on![]() then the function
then the function![]() has a local maximum on
has a local maximum on![]()