If we iterate a function – find![]() etc with the nth iteration written
etc with the nth iteration written![]() – it may have one of these behaviours:
– it may have one of these behaviours:
-
The iterated function may tend to infinity: If
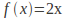 then
then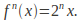
-
The iterated function may tend to a limit:
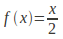 then
then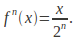
-
The iterated function may be constant:
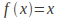 so
so
-
The iterated function may cycle:
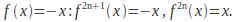
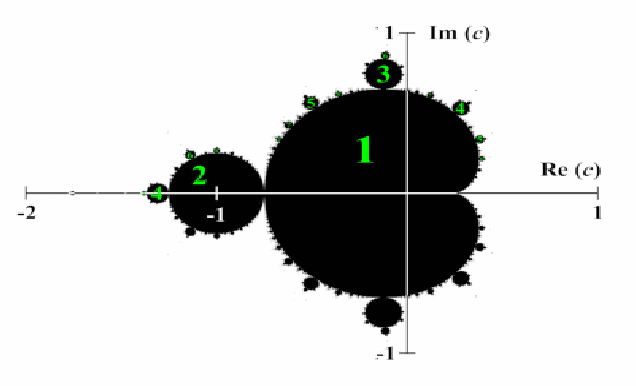
The Mandlebrot set concerns the family of quadratic functions![]() If we define the iteration relation
If we define the iteration relation![]() then the Mandlebrot set illustrates those values of
then the Mandlebrot set illustrates those values of![]() for which
for which![]() does not iterate to infinity.
does not iterate to infinity.
Features of the Mandlebrot Set
-
The Mandlebrot Set is a connected subset of
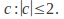
-
Is symmetric under reflection in the
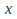 axis.
axis. -
Meets the real axis in the interval
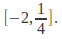
-
Has no holes in it.
-
Little copies of the whole Mandlebrot set appear all over the diagram in a manner characteristic of fractals.