Let![]() form a
form a![]() – cycle of an analytic function
– cycle of an analytic function![]() Then
Then
-
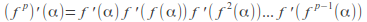
-
The derivative of
 takes the same value at each point of the
takes the same value at each point of the – cycle so tha
– cycle so tha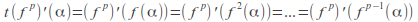
Proof
Since![]() where the function
where the function![]() is applied p times, we can deduce using the Chain Rule that
is applied p times, we can deduce using the Chain Rule that![]()
Putting![]() gives 1 above.
gives 1 above.
![]() is the product of the derivatives of
is the product of the derivatives of![]() at the points of the
at the points of the![]() – cycle so
– cycle so![]() is also the product of the derivatives of
is also the product of the derivatives of![]() at the points of the
at the points of the![]() – cycle and similarly for the other points
– cycle and similarly for the other points![]()
The derivative of![]() at the point of a
at the point of a![]() – cycle determines the nature of the point. Part 2 above implies that all the points of a
– cycle determines the nature of the point. Part 2 above implies that all the points of a![]() - cycle have the same nature and we can talk of the nature of the
- cycle have the same nature and we can talk of the nature of the![]() – cycle as a whole.
– cycle as a whole.
If![]() is a periodic point with period
is a periodic point with period![]() of an analytic function
of an analytic function![]() then
then![]() and the corresponding
and the corresponding![]() – cycle are
– cycle are
attracting if![]()
repelling if![]()
indifferent if![]()
super attracting if![]()
Example: If![]() then the period 2 – points are
then the period 2 – points are![]() and
and![]()
![]() s
s![]() and
and![]()
![]() so
so![]() and the 2 – cycle consisting of the points
and the 2 – cycle consisting of the points![]() and
and![]() is repelling.
is repelling.