The Radius and Centre of a Circle in Apollonian Form

Letbe the generalized circle with  equationwithand

Ifthenis the circle with centreand radiuswhereand

Alsolies on the line throughand and

Ifthenis the line throughperpendicular to

Proof

Letbe the extended mobius transformation defined by

maps the circle defined byto the unit circle and somaps the unit circle toso that and

Sincepoints on the extended real axis are mapped byto points on the extended linethroughand

Ifthen the diametrically opposite points -1 and 1 are mapped byto the diametrically opposite pointsandofonbecauseis conformal at 1 and -1.

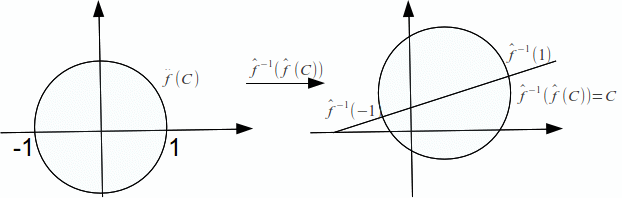
It follows thathas centreongiven byand radius given by

Furthermore

Ifthensomust be a line that meetsin a right angle at