The Radius of Convergence Theorem
For a given power series,![]() precisely one of the following may happen
precisely one of the following may happen
the series converges only for
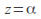
the series converges for all
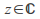
there is some real number
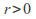 such that
such that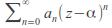 converges and converges absolutely if
converges and converges absolutely if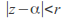 and
and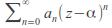 diverges if
diverges if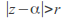
Example: find the radius of convergence of the sequence![]()
![]() in this example. The ratio test demands
in this example. The ratio test demands![]() for convergence so
for convergence so![]()
As![]() so
so![]() and as
and as![]() the right hand side tends to 0 so the sequence converges only for
the right hand side tends to 0 so the sequence converges only for![]() The radius of convergence is 0.
The radius of convergence is 0.
Example: find the radius of convergence of the sequence![]()
The ratio test demands![]() for convergence so
for convergence so![]()
As![]() for all
for all![]() so the sequence converges for all
so the sequence converges for all![]()
Example: find the radius of convergence of the sequence![]()
The ratio test demands![]() for convergence so
for convergence so![]()
The radius of convergence is 1.