The Riemann mapping theorem states that if![]() is a non-empty simply connected region in
is a non-empty simply connected region in![]() and
and![]() then there exists a bijective and holomorphic function
then there exists a bijective and holomorphic function![]() from
from![]() onto the open unit disk
onto the open unit disk![]()
The condition that![]() be simply connected means that
be simply connected means that![]() does not contain any “holes”. The fact that f is bijective and holomorphic implies that it is a conformal map so preserves angles between lines or vectors and also the shape of any sufficiently small figure, possibly rotating and scaling it.
does not contain any “holes”. The fact that f is bijective and holomorphic implies that it is a conformal map so preserves angles between lines or vectors and also the shape of any sufficiently small figure, possibly rotating and scaling it.
Poincaré proved that the function![]() is unique: if
is unique: if![]() and
and![]() is an arbitrary angle, then there exists a unique
is an arbitrary angle, then there exists a unique![]() as above with the additional properties that
as above with the additional properties that![]() and that
and that![]() This is an easy consequence of the Schwarz lemma.
This is an easy consequence of the Schwarz lemma.
As a corollary, any simple, connected subsets of![]() can be mapped to each other because given
can be mapped to each other because given![]() there exists a bijective holomorphic function
there exists a bijective holomorphic function![]() mapping
mapping![]() to
to![]() and given
and given![]() there exists a bijective holomorphic function
there exists a bijective holomorphic function![]() mapping
mapping![]() to
to![]() then since
then since![]() is bijective,
is bijective,![]() exists and
exists and![]() maps
maps![]() to
to![]()
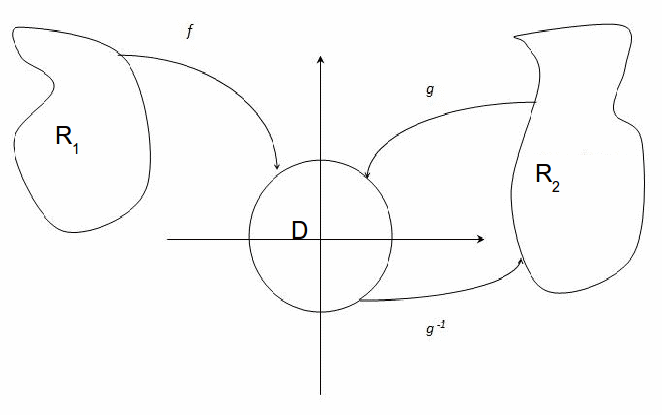
Further, since there exists a bijective mapping from the Riemann sphere onto![]() any two simply connected regions of the Riemann sphere can be mapped to each other.
any two simply connected regions of the Riemann sphere can be mapped to each other.