The Riemann sphere is the geometric representation of the extended complex plane![]() obtained by placing a unit spehre at the origin. For each point in the plane, a line is drawn from that point to the North Pole. The line will intersect the sphere at a single, unique point. We can represent the point
obtained by placing a unit spehre at the origin. For each point in the plane, a line is drawn from that point to the North Pole. The line will intersect the sphere at a single, unique point. We can represent the point![]() in the natural way as the North Pole.
in the natural way as the North Pole.
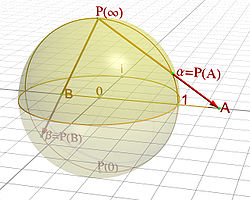
If![]() is a point in the plane, it projects to the point
is a point in the plane, it projects to the point![]()
Conversely a pount (u,v,w) on the sphere satisfies![]()
The inverse transformation can be easily derived.
Consider the component of the inverse transformation along the real axis.
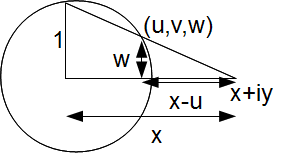
Consideration of similar triangles gives![]() similarly for
similarly for![]()
![]() and
and![]()
To find P(x,y), we write
![]()
Now![]()
Also![]()
Hence![]()