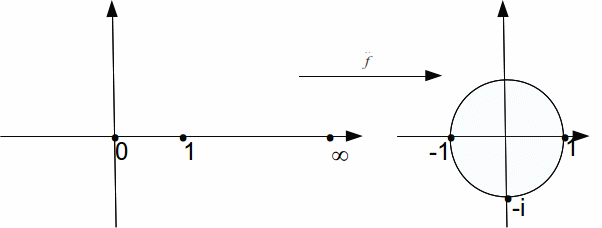
The Three Point Trick
The Three Point Trick is a method of finding the equation of the image of a generalized circle – a circle or line (a line can be considered a circle of infinite radius) – after a generalized mobius transformation. Any circle is completely defined by three distinct points that lie on it, and any line is defined by two distinct points (the point at infinity must lie on a line. This can be considered a third point since a line is a circle of infinite radius).
To find the image of a generalized circle C under an extended mobius transformation hat f it is sufficient to find the image of three distinct points that lie on C.
Example: Find the image of the circle![]() under the extended mobius transformation
under the extended mobius transformation![]()
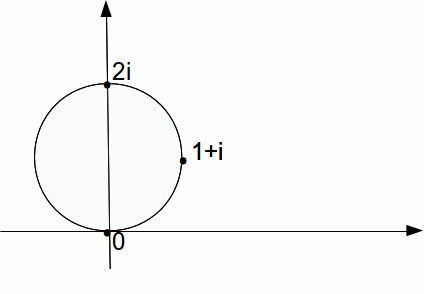
Find the images of those points under the transformation.
![]()
![]()
![]()
The image of the circle is shown below.
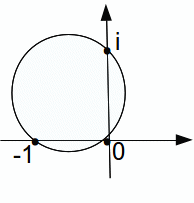
This circle has the equation![]()
If the circle passes through the pole of the transformation (if it has one) then a circle will map to a line.
Example: Find the image of the extended line![]() under the extended mobius transformation
under the extended mobius transformation![]()
The points![]() and
and![]() lie on the line. The images of these points are
lie on the line. The images of these points are
![]()
![]()
![]()
The image of the extended line is the unit circle![]()