Green's theorem gives the relationship between a line integral around a simple closed curve![]() and a double integral over the plane region
and a double integral over the plane region![]() bounded by
bounded by![]() It is the two-dimensional special case of the more general Stokes' theorem, and is named after British mathematician George Green.
It is the two-dimensional special case of the more general Stokes' theorem, and is named after British mathematician George Green.
Let![]() be a positively oriented (counterclockwise), piecewise smooth, simple closed curve in the plane
be a positively oriented (counterclockwise), piecewise smooth, simple closed curve in the plane![]() and let
and let![]() be the region bounded by
be the region bounded by![]() If
If![]() and
and![]() are functions of
are functions of![]() defined on an open region containing
defined on an open region containing![]() and have continuous partial derivatives there, then
and have continuous partial derivatives there, then![]()
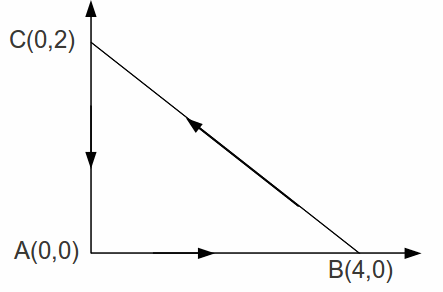
For example let![]() be the triangular region illustrated below and let
be the triangular region illustrated below and let![]()
![]()
We need to find the limits. If we integrate with respect to![]() first then we must find
first then we must find![]() as a function of
as a function of![]() on the line BC:
on the line BC:![]() Our integral becomes
Our integral becomes
![]()
Expanding the integrand and simplifying gives
![]()
![]()