Legendre's Equation - Legendre Polynomials

The second order, non constant coefficient, differential equationwith boundary conditionis finite is known as Legendre's equation. Solutions exist forand the normalized solutions,are polynomials of degreeknown as Legendre polynomials. These polynomials are defined only on the intervalbecause ator 1 the coefficient ofis zero.

The first few Legendre polynomials are given by

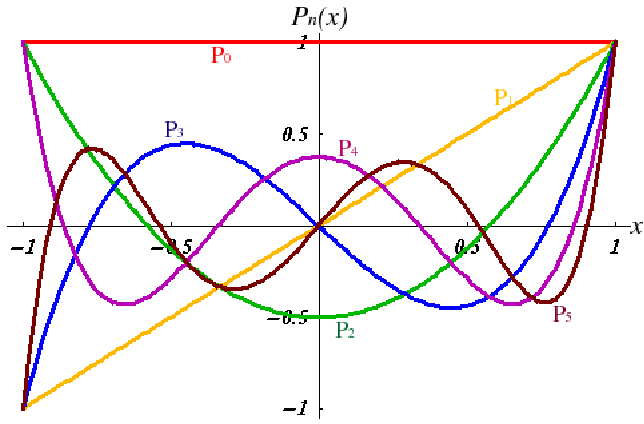
Legendre polynomials form a mutually orthonormal set, that iswhere

Proof: The P-n (x) satisfy

We can write this as(1)

Similarly, for a solutionwe can write(2)

Multiply (1) byand integrate between -1 and 1:

Integrating the first term by parts gives

The first term on the right is zero:

Similarly for (2)

The right hand side of both equations are the same so

Sincewe must have both sides are zero hence