The second order, non constant coefficient, differential equation![]() with boundary condition
with boundary condition![]() is finite is known as Legendre's equation. Solutions exist for
is finite is known as Legendre's equation. Solutions exist for![]() and the normalized solutions,
and the normalized solutions,![]() are polynomials of degree
are polynomials of degree![]() known as Legendre polynomials. These polynomials are defined only on the interval
known as Legendre polynomials. These polynomials are defined only on the interval![]() because at
because at![]() or 1 the coefficient of
or 1 the coefficient of![]() is zero.
is zero.
The first few Legendre polynomials are given by
![]()
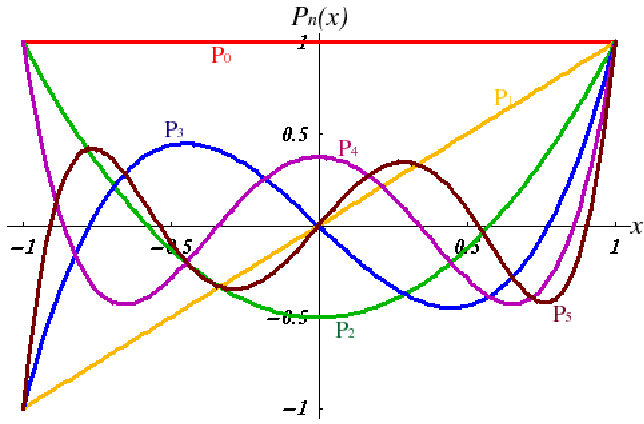
Legendre polynomials form a mutually orthonormal set, that is![]() where
where ![]()
Proof: The P-n (x) satisfy![]()
We can write this as![]() (1)
(1)
Similarly, for a solution![]() we can write
we can write![]() (2)
(2)
Multiply (1) by![]() and integrate between -1 and 1:
and integrate between -1 and 1:
![]()
Integrating the first term by parts gives![]()
The first term on the right is zero:
![]()
Similarly for (2)![]()
The right hand side of both equations are the same so
![]()
Since![]() we must have both sides are zero hence
we must have both sides are zero hence![]()