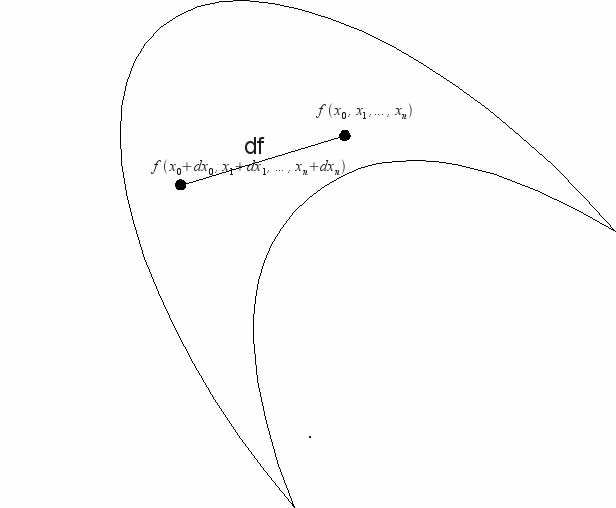
If f is a function of several variables, the total differential enables us to find the change in f as the function moves a small distance between two points
and
We find all the partial derivatives
then the total derivative
(1) and this is roughly equal to
with the degree of accuracy increasing asand get closer together.
We evaluate (1) at
Example: If
find
and estimate the change in
asmoves along a curve between
and
With
and