Volume Bounded by a Surface and a Region in the Plane
Suppose we have a surface\[z=f(x,y\]
where \[z\]
is the height of the surface above the \[xy\]
plane.
\[R\]
in the \[xy\]
plane is \[V = \int_R f(x,y) dx dy\]
.Example: Find the volume bounded by the surface
\[z=x^3 + y^3\]
and the triangle in the \[xy\]
plane between the coordinates \[(0,0,0), ((1,1,0), (1,0,0)\]
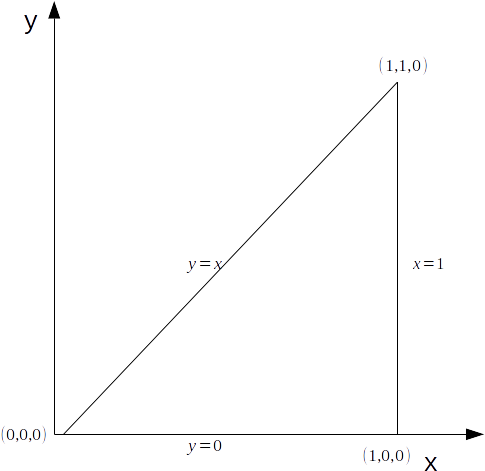
\[x=0, x=1, y=x\]
so we can write as the region of integration as \[0 \leq x \leq 1 , y \leq x\]
The integral becomes
\[\begin{equation} \begin{aligned} V &= \int^1_0 \int^x_0 (x^3 +y^3) dy dx \\ &= \int^1_0 [x^3 y + y^4/4]^x_0 dx \\ &= \int^1_0 5x^4/4 dx \\ &= [x^5/4]^1_0 \\ &= 1/4 \end{aligned} \end{equation} \]