The busy beaver problem is to find a Turing machine that writes the maximum number of 1's on a strip of tape then halts. The n – state Turing machine that writes the largest possible number of 1's is called an n-state busy beaver, More formally, given an
- state Turing Machine with a two symbol alphabet
what is the maximum number of 1's that the machine may print on an initially blank tape (0 - filled) before halting?
It turns out that this problem can't be solved in general. It is non-computable and this implies that it is undecidable by a general algorithm whether an arbitrary Turing machine is a busy beaver.
Mathematicians have solved it for
(for Turing Machines with 1, 2, 3 and 4 states) by running all possible Turing Machines for these values of
but the complexity increases dramatically with n, and it is doubted that the problem will ever be solved for
Denote the number of 1s that the busy beaver writes on a tape after halting as
and call it the busy beaver function (the solution to the busy beaver problem). The busy beaver function is also interesting -- it grows faster than any computable function. It grows like this:
-
-
-
-
-
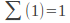
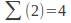
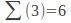
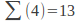
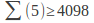(the exact result has not been found) -
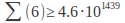(the exact result may never be known)
If we were to use one atom for each 1 that the busy beaver puts on the tape, at
there would be more 1's than there are atoms in the universe.
There are finitely many Turing machines withstates and 2 symbols (
such). In addition it is trivial that some of these are halting machines; i.e., there exists at least one- state, 2 - symbol Turing Machine that will halt for every
Define:
-
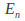as the finite, non-empty set of halting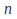- state 2 - symbol Turing machines. -
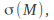for each Turing machine
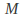in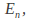
is the score of machine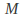- the number of 1's finally on the tape after machine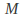is run to completion with an initially blank tape. -
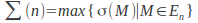(i.e., the maximum score among all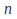- state 2-symbol halting Turing machines started with a blank tape).
Since
is a non-negative integer for any
and since
is a non-empty finite set,
is a well-defined non-negative integer for every nonnegative integer