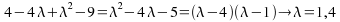Eigenvalues
Given a linear transformation A , a non-zero vector x is defined to be an eigenvector of the transformation if it satisfies the eigenvalue equation
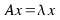 (1)
(1) - for some scalar
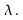 In this situation, the scalar
In this situation, the scalar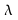 is called an "eigenvalue" of A corresponding to the eigenvector
is called an "eigenvalue" of A corresponding to the eigenvector In other words the result of multiplying
In other words the result of multiplying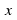 b y the matrix is just a scalar multiple
b y the matrix is just a scalar multiple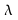 of
of
The key equation in this definition is the eigenvalue equation,![]() Most vectors
Most vectors![]() will not satisfy such an equation: a typical vector changes direction when acted on by A , so that
will not satisfy such an equation: a typical vector changes direction when acted on by A , so that![]() is not a multiple of
is not a multiple of![]() This means that only certain special vectors are eigenvectors, and only certain special scalars
This means that only certain special vectors are eigenvectors, and only certain special scalars![]() are eigenvalues. Of course, if A is a multiple of the unit matrix, then no vector changes direction, and all non-zero vectors are eigenvectors.
are eigenvalues. Of course, if A is a multiple of the unit matrix, then no vector changes direction, and all non-zero vectors are eigenvectors.
The requirement that the eigenvector be non-zero is imposed because the equation![]() holds for every A and every
holds for every A and every![]() Since the equation is always trivially true, it is not an interesting case. In contrast, an eigenvalue can be zero in a nontrivial way. Each eigenvector is associated with a specific eigenvalue. One eigenvalue can be associated with several or even with an infinite number of eigenvectors.
Since the equation is always trivially true, it is not an interesting case. In contrast, an eigenvalue can be zero in a nontrivial way. Each eigenvector is associated with a specific eigenvalue. One eigenvalue can be associated with several or even with an infinite number of eigenvectors.
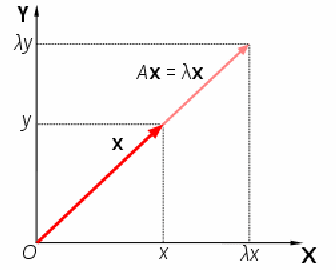
![]() acts to stretch the vector
acts to stretch the vector![]() not change its direction, so
not change its direction, so![]() is an eigenvector of A .
is an eigenvector of A .
From (1)![]() which we may factorise as
which we may factorise as![]() hence Det
hence Det![]() where I is the identity matrix.
where I is the identity matrix.
- We may then form a polynomial equation in
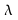 and solve it to find the eigenvalues:
and solve it to find the eigenvalues: - A=
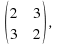 A-λI=
A-λI=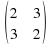 -
- 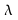
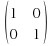 which becomes
which becomes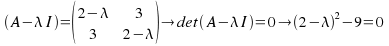
We can simplify, factorise and solve.
-