A transformation may be represented by a matrix
operating on a vector
where
is the position vector of a point P. The resulting transformed position vector is
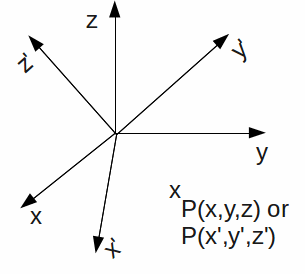
It is important to note that the position of the point
does not change in space, only the representation of the point with respect to the new coordinate system. We may consider the matrix acting to change the basis of the space into a new basis.
Suppose the transformation T is represented by the matrix
If the original coordinate system has basis vectors
called the standard basis
then the transformed basis vectors are given by
and
We may write a point with position vector
as
We can find a similar representation in the new coordinate system for a vector
in terms of
and
Suppose we have a vector
We can write
so
Hence
This is general. If the matrix representing a change of basis is
the basis vectors
and
transform as
and
but the components
and
transform as
and 
respectively.