A transformation may be represented by a matrix![]() operating on a vector
operating on a vector![]() where
where![]() is the position vector of a point P. The resulting transformed position vector is
is the position vector of a point P. The resulting transformed position vector is![]()
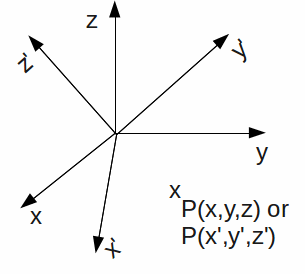
It is important to note that the position of the point![]() does not change in space, only the representation of the point with respect to the new coordinate system. We may consider the matrix acting to change the basis of the space into a new basis.
does not change in space, only the representation of the point with respect to the new coordinate system. We may consider the matrix acting to change the basis of the space into a new basis.
Suppose the transformation T is represented by the matrix![]() If the original coordinate system has basis vectors
If the original coordinate system has basis vectors![]() called the standard basis
called the standard basis
then the transformed basis vectors are given by![]() and
and![]()
We may write a point with position vector![]() as
as![]()
We can find a similar representation in the new coordinate system for a vector![]() in terms of
in terms of![]() and
and![]()
Suppose we have a vector![]() We can write
We can write![]() so
so![]()
Hence![]()
This is general. If the matrix representing a change of basis is![]() the basis vectors
the basis vectors![]() and
and![]() transform as
transform as![]() and
and![]() but the components
but the components![]() and
and![]() transform as
transform as![]() and
and ![]() respectively.
respectively.