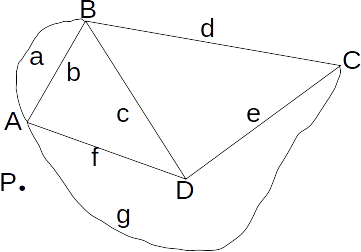
We can represent each arc taken anticlockwise about a point P by a vector.
\[a= \begin{pmatrix}1\\0\\0\\0\\0\\0\\0\end{pmatrix}, \: b= \begin{pmatrix}0\\1\\0\\0\\0\\0\\0\end{pmatrix}, \: c= \begin{pmatrix}0\\0\\1\\0\\0\\0\\0\end{pmatrix}, \: d= \begin{pmatrix}0\\0\\0\\1\\0\\0\\0\end{pmatrix}, \: e= \begin{pmatrix}0\\0\\0\\0\\1\\0\\0\end{pmatrix}, \: f= \begin{pmatrix}0\\0\\0\\0\\0\\1\\0\end{pmatrix}, \: g= \begin{pmatrix}0\\0\\0\\0\\0\\0\\1\end{pmatrix}\]
Then arc bcf is
\[-b-c+f= \begin{pmatrix}0\\-1\\-1\\0\\0\\1\\0\end{pmatrix}\]
and the arc cde by the vector
\[c-d-e= \begin{pmatrix}0\\0\\1\\-1\\-1\\0\\0\end{pmatrix}\]
Adding these gives
\[-b-c+f+c-d-e=-b+f-d-e= \begin{pmatrix}0\\0\\-1\\0\\-1\\-1\\1\end{pmatrix}\]
.