Closure of the Reciprocal Sequence in a Metric Space
Theorem
Let![]() be the space of real numbers in the metric space
be the space of real numbers in the metric space![]() with the absolute value metric
with the absolute value metric![]() and let
and let![]()
The closure of![]() is
is![]() and the closure of any subset
and the closure of any subset![]() of
of![]() is a closed subset of
is a closed subset of![]()
Proof
Let![]() The closure of
The closure of![]() written
written![]() is defined as
is defined as![]() where
where ![]()
Since![]()
For each![]()
Hence![]() and
and![]()
Choose![]() and
and![]() then
then![]() hence
hence![]()
To prove the closure of any subset![]() of
of![]() is a closed subset of
is a closed subset of![]() suppose
suppose![]() is not closed then
is not closed then![]() is not open and there is an element
is not open and there is an element![]() such that for every
such that for every![]()
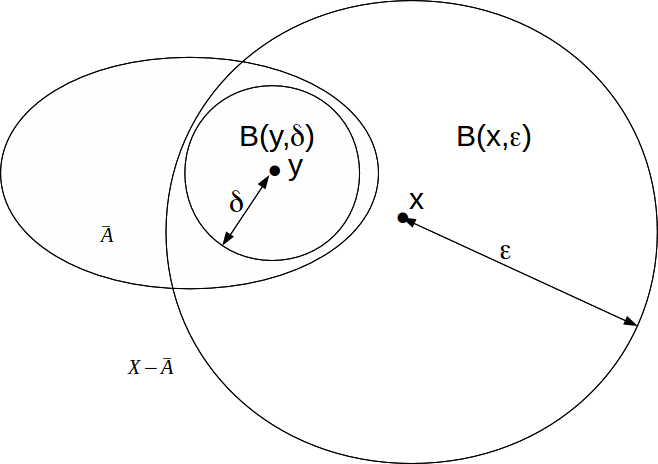
Choose![]()
Since![]() is open there exists
is open there exists![]() such that
such that![]()
Since![]() then
then![]() so
so![]() exists such that
exists such that![]()
Hence for![]() there exists
there exists![]() such that
such that![]() Hence
Hence![]() contradicting
contradicting![]()