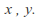A metric space is a set of points where the distance between any two points
can be calculated with a function of the coordinates of the points, called a metric:
The metric space which most closely corresponds to our intuitive understanding of space is the ordinary Euclidean space, in one, two, three of more dimensions. In fact, the notion of "metric" is a generalization of the Euclidean metric, which defines the distance between two points as the length of the straight line segment connecting them.
The geometric properties of the space depend on the metric chosen, and by using a different metric we can construct non-Euclidean geometries such as those used in the theory of general relativity.
The metric must satisfy three properties:
M1: If
then
If
then
M2:
The distance between two points is a number which does not depend on how the points are oriented.
M3:
where
are any three points in the space. This is a generalization of the triangle inequality.
Examples:
-
The real numbers with the metric
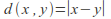which returns the magnitude of the difference between two numbers.
-
If
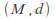is a metric space and
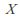is a subset of
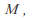then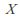becomes a metric space by restricting
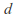to 
.
-
The discrete metric, where
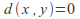if
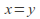and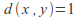
is a metric. Any non empty set can be made into a metric space with this metric. Any point in the space is an open ball, and therefore every subset is open and the space has the discrete topology.
-
If
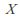is some set and
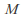is a metric space, then the set of all bounded functions
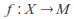(i.e. those functions whose image is a bounded subset of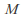) can be turned into a metric space by defining
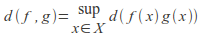for any two bounded functions
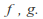Here sup is the supremum.
-
If
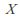is a topological (or metric) space and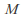is a metric space, then the set of all bounded continuous functions from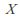to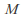forms a metric space if we define the metric as above: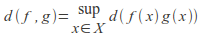for any two bounded continuous functions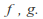If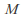is complete, then this space is complete as well.
-
The set V of vertices of an undirected graph G can be turned into a metric space by defining
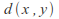to be the length of the shortest path connecting the vertices