Three basic metrics are illustrated below in ordinary two dimensional Euclidean space. Each metric illustrates the the locus described by![]()
For![]()
For![]()
For![]()
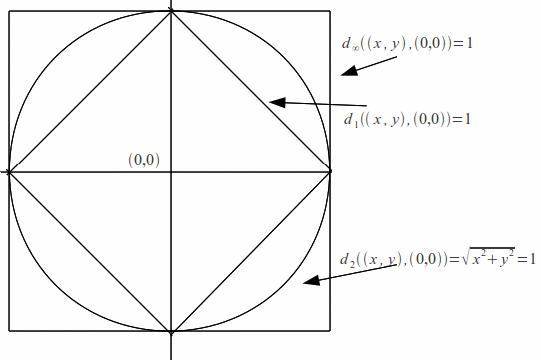
All of the metrics above are topologically equivalent. They all give rise to the same metric space, with the same open sets.. This is easy to prove since each metric obeys the %epsilon - %delta criterion. On the other hand the discrete metric
![]()
is not topologically equivalent, giving rise to the discrete metric space where each singleton set is open.
In addition, we can define function spaces. Each point in the space is a function, with the metric typically defined in terms of the difference between two functions on an underlying space. The metrics are similar to those above.
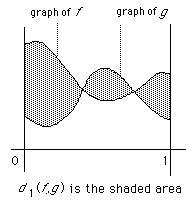
For example![]() for bounded functions defined on
for bounded functions defined on![]() shown below.
shown below.
![]()
![]() shown below.
shown below.
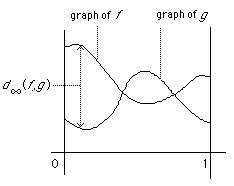
![]()