Proof that the Smallest Closed Set Containing a Set is the Closure of the Set

Theorem

Ifis a set, the smallest closed set containing is the closure of

We can also writewhereis closed andfor each

Proof

Letbe a set andsuch that

SupposeandSince eachis closedis also closed andis open.

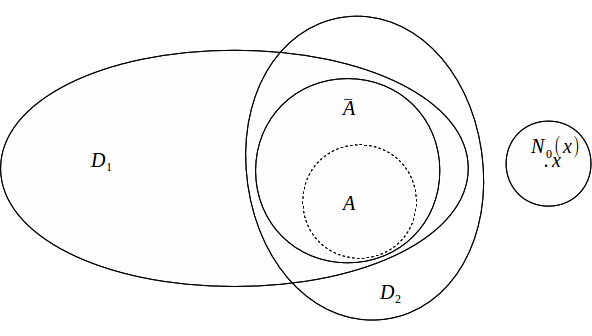
Hence x has a neighbourhoodofsuch that

Now we must proveSupposethen there is a neighbourhoodof such that

Thereforeis closed and containsfor some

Since