For any real or complex
and any integer
we define
\[\sigma_{\alpha}(n)= \sum_{d | n}d^{\alpha}\]
is the sum of the
powers of
The functions
are called divisor functions. They are multiplicative because
the Dirichlet product of two multiplicative functions, but not completely multiplicative.
When
is the number of divisors of
When
is the sum of the divisors of
When
is the sum of the reciprocals of the divisors of
Since
is multiplicative we have
To compute
note that the divisors of
are 
hence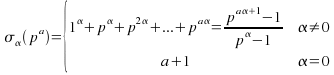
Becauseis multiplicative (but not completely multiplicative) we can also write
If
then 
The Dirichlet inverse ofcan also by expressed as a linear combination of the
powers of the divisors of
Theorem
For
we have
Proof: Since
and
is completely multiplicative we have