For any real or complex![]() and any integer
and any integer![]() we define
we define
\[\sigma_{\alpha}(n)= \sum_{d | n}d^{\alpha}\]
![]() is the sum of the
is the sum of the![]() powers of
powers of![]()
The functions![]() are called divisor functions. They are multiplicative because
are called divisor functions. They are multiplicative because![]() the Dirichlet product of two multiplicative functions, but not completely multiplicative.
the Dirichlet product of two multiplicative functions, but not completely multiplicative.
When![]() is the number of divisors of
is the number of divisors of![]()
When![]() is the sum of the divisors of
is the sum of the divisors of![]()
When![]() is the sum of the reciprocals of the divisors of
is the sum of the reciprocals of the divisors of![]()
Since![]() is multiplicative we have
is multiplicative we have![]()
To compute![]() note that the divisors of
note that the divisors of![]() are
are ![]() hence
hence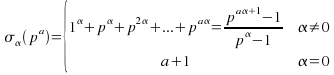
Because![]() is multiplicative (but not completely multiplicative) we can also write
is multiplicative (but not completely multiplicative) we can also write
![]()
If![]() then
then ![]()
![]()
The Dirichlet inverse of![]() can also by expressed as a linear combination of the
can also by expressed as a linear combination of the![]() powers of the divisors of
powers of the divisors of![]()
Theorem
For![]() we have
we have![]()
Proof: Since![]() and
and![]() is completely multiplicative we have
is completely multiplicative we have![]()