Prime Numbers
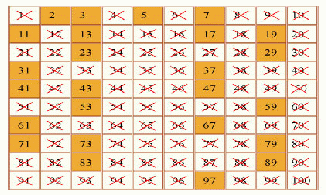
Primes numbers are used much in codes and cryptography. The primes numbers less than 100 are coloured orange in the following number square,.
A number![]() is a prime number if
is a prime number if![]() and the only positive divisors of
and the only positive divisors of![]() are 1 and
are 1 and![]() If
If ![]() and
and![]() is not prime then it is called composite. Prime numbers are usually denoted by some variation on the letter
is not prime then it is called composite. Prime numbers are usually denoted by some variation on the letter![]() or
or![]()
The prime numbers less than 50 are 2,3,5,7,11,13,17,19,23,29,31,37,42,43,47.
Theorem 1
Every integer![]() is either a prime number or a product of prime numbers.
is either a prime number or a product of prime numbers.
Proof: Use induction on![]() The theorem is clearly true for
The theorem is clearly true for![]() Assume it is true for every
Assume it is true for every![]() . If
. If![]() is not prime it has a positive divisor
is not prime it has a positive divisor![]() hence
hence![]() where
where![]() But both
But both![]() so each of
so each of![]() are products are prime numbers hence so is
are products are prime numbers hence so is![]()
Theorem 2
There are infinitely many prime numbers.
Proof (originally due to Euclid): Suppose there are only a finite number, say![]() Let
Let ![]() Now
Now![]() so either
so either![]() is prime or
is prime or![]() is a product of primes. Of course
is a product of primes. Of course![]() is not prime since it exceeds
is not prime since it exceeds![]() for
for![]() Moreover, no
Moreover, no![]() divides
divides![]() (if
(if![]() divides
divides![]() then
then![]() divides the difference
divides the difference![]() This contradicts theorem 1.
This contradicts theorem 1.
Theorem 3
If a prime![]() does not divide
does not divide![]() then
then![]()
Proof: Let![]() then
then![]() divides
divides![]() so
so![]() or
or![]() but
but![]() so
so![]() because
because ![]() hence
hence![]()
The above theorem implies also that the only divisors of p are 1 and p, the definition of prime numbers.
Theorem 4
If a prime![]() divides
divides![]() then
then![]() or
or![]() More generally if a prime
More generally if a prime![]() divides a product
divides a product![]() then
then![]() divides at least one of the factors.
divides at least one of the factors.
Proof: Assume![]() divides
divides![]() and
and![]() By theorem 3
By theorem 3![]() so by Euclid's Lemma,
so by Euclid's Lemma,![]()