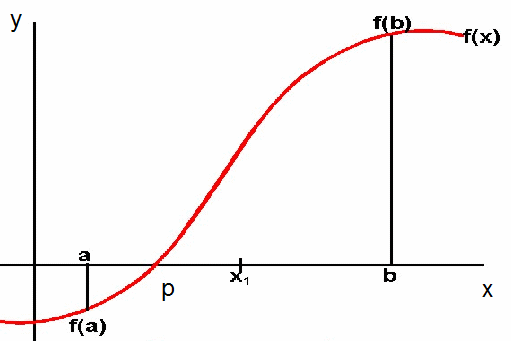
Suppose![]() isa continuous function on some interval
isa continuous function on some interval![]() with
with![]() and
and![]() of opposite sign. By the intermediate value theorem, there is
of opposite sign. By the intermediate value theorem, there is![]() suchthat
suchthat![]() For simplicity, let's assume there exists only one root in
For simplicity, let's assume there exists only one root in![]() as shown.
as shown.
Bisection gives a simple and robust method for bracketing the root![]() The algorithm works as follows:
The algorithm works as follows:
Take the midpoint![]() as a first guess and calculate
as a first guess and calculate![]() If
If![]() and
and![]() are
are
of opposite sign then the root lies in the interval![]() (Conversely,if
(Conversely,if![]() has the opposite
has the opposite
sign to![]() then the root lies in the interval
then the root lies in the interval![]() )
)
This procedure can be repeated iteratively, e.g. taking a second guess![]() from
from
the example above.
At each iteration we halve the size of the interval![]() that contains the root
that contains the root![]() and after n
and after n
iterations of the procedure we have reduced the uncertainty in![]() down to,
down to,
![]()
Example: The function![]() has a root in the interval
has a root in the interval![]() since
since![]() and
and![]() The actual root is of course
The actual root is of course![]()
|
0.00000 |
0.00000 |
0.00000 |
0.00000 |
0.00000 |
0.00000 |
0.00000 |
|
1.00000 |
0.00000 |
6.00000 |
3.00000 |
3.50000 |
3.00000 |
1.58600 |
|
2.00000 |
0.00000 |
3.00000 |
1.50000 |
0.12500 |
1.50000 |
0.08600 |
|
3.00000 |
0.00000 |
1.50000 |
0.75000 |
-0.71900 |
0.75000 |
0.66400 |
|
4.00000 |
0.75000 |
1.50000 |
1.12500 |
-0.36700 |
0.37500 |
0.28900 |
|
5.00000 |
1.12500 |
1.50000 |
1.31250 |
-0.13900 |
0.18750 |
0.10200 |
|
6.00000 |
1.31250 |
1.50000 |
1.40625 |
-0.01100 |
0.09375 |
0.00800 |
In the table,![]() and
and![]() is the exact absolute error.
is the exact absolute error.
Advantages of the method
i. provided the function is continuous on an interval![]() with
with![]() bisection is
bisection is
guaranteed to work.
ii. the number of iterations needed to achieve a specific accuracy is known in advance.
Disadvantages of the method :
i. the method is slow to converge.
ii. the errors in![]() and in
and in![]() do not necessarily decrease between iterations. Note that,
do not necessarily decrease between iterations. Note that,
in the example above![]() is closer to
is closer to![]() (and
(and![]() closer to 0) than the next 3 iterates.
closer to 0) than the next 3 iterates.
Also, no advantage is taken of intermediate good approximations.