Interpolation may used to approximate either a known function or a set of data for an unknown function. It is not possible to evaluate the error for an unknown function.
If![]() (i.e.
(i.e.![]() is a function
is a function![]() times differentiable in
times differentiable in![]() with continuous derivatives) and
with continuous derivatives) and![]() is the polynomial that interpolates
is the polynomial that interpolates![]() then
then![]() there exists
there exists![]() that depends on
that depends on![]() such that
such that
![]()
Proof: This result is trivially true for![]() since both sides are zero.
since both sides are zero.
For![]() define
define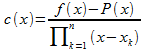 so that
so that![]()
Define the function
![]()
which satisfies![]() for
for![]() and
and![]()
![]() has
has![]() distinct roots in
distinct roots in![]()
By Rolle's theorem, there must be at least one root of![]() between two successive roots of
between two successive roots of![]() So
So![]() has at least
has at least![]() distinct roots in
distinct roots in![]()
Apply Rolle's theorem to derivatives of increasing order successively, to show that![]() must have at least one root in
must have at least one root in![]() Call this point
Call this point![]() so that
so that![]()
The nth derivative of![]() is
is![]() but
but![]() is a polynomial of degree
is a polynomial of degree![]() so
so![]()
Let![]() so that
so that![]()
Hence![]()
Using this we can obtain bounds on the accuracy of Lagrange interpolation, provided we can bound the nth derivative,![]() Since the error term involves
Since the error term involves![]() Lagrange interpolation is exact for polynomials of degree
Lagrange interpolation is exact for polynomials of degree![]() at most.
at most.
Example: Estimate the error for f(x)= sin(3x) interpolated for the points
![]() at
at![]()
![]()
So, the error in the approximation to![]() is
is![]()
The actual error is![]()
However, the function![]() cannot be approximated accurately by an interpolation
cannot be approximated accurately by an interpolation
polynomial, using equidistant points on the interval![]() Although
Although![]() is differentiable, its derivatives grow as
is differentiable, its derivatives grow as![]() for
for![]() even so
even so![]() does not converge to 0 while
does not converge to 0 while![]() increases (since interval width > 1).
increases (since interval width > 1).