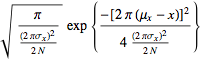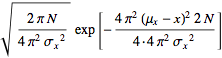Proof of Central Limit Theorem

The central limit theorem is one of the most important theorems in statistics. It approximates the distribution of the meanof any sample of size n from any distribution by the distribution

Now write

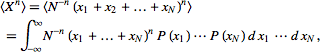
so we have

Now expand so

since

Taking the Fourier transform,

This is of the form

where and.

But this is a Fourier transform of a Gaussian function, so

Therefore,

But and, so