If the random variable![]() is described by a normal distribution
is described by a normal distribution![]() then the distribution of
then the distribution of![]() is descibed by a probability density function
is descibed by a probability density function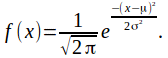
Differentiating this gives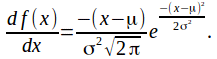
Differentiating again (using the product rule) gives
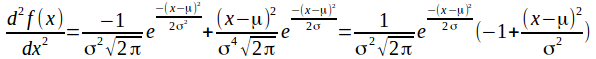
Since![]()
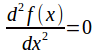 if and only if
if and only if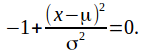
Hence![]() or
or![]()
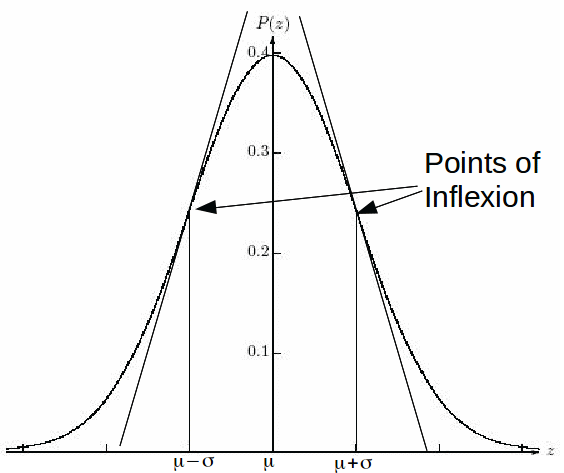
The points of inflexion are shown below (note that a point of inflexion is such that the curve crosses a tangent at a point).