Definition: Axiom of Choice. Let![]() be a collection of nonempty sets. Then we can choose a element from each set
be a collection of nonempty sets. Then we can choose a element from each set![]() so that there exists a function
so that there exists a function![]() (called a choice function) defined on
(called a choice function) defined on![]() with the property that, for each set
with the property that, for each set![]()
Initially controversial, it is now a basic assumption used in many areas of maths. It is independent of the other axioms of set theory. Thus there are no contradictions in choosing to reject it and choosing another instead. The axiom can be stated in many equivalent ways. For example:
-
The cardinality of any of two sets is less than or equal to the cardinality of the other. one set has cardinality less than or equal to that of the other. This implies there exists a bijection from one set to a subset of the other.
-
Any vector space over a field
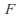 has a basis -- a maximal linearly independent subset -- over that field.
has a basis -- a maximal linearly independent subset -- over that field. -
Any product of compact topological spaces is compact.
-
The axiom of choice is equivalent to the well-ordering principle.
Examples of choice functions
-
If
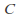 is the collection of all nonempty subsets of
is the collection of all nonempty subsets of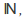 then
then 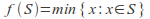 is one possible choice function.
is one possible choice function. -
If
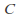 is the collection of all bounded intervals of
is the collection of all bounded intervals of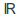 we can let
we can let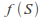 be the midpoint of the interval
be the midpoint of the interval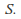
-
No choice function has ever been found when
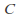 is the collection of all nonempty subsets of the real numbers, and it may be that non exists.
is the collection of all nonempty subsets of the real numbers, and it may be that non exists.