Alternative Proof of Euler Characteristic of Sphere With n Handles
Start with a sphere with n handles. Draw a map with vertices and edges at each join of a handle with the sphere. Detach one end of each handle, making each handle a 'cuff' and a hole.
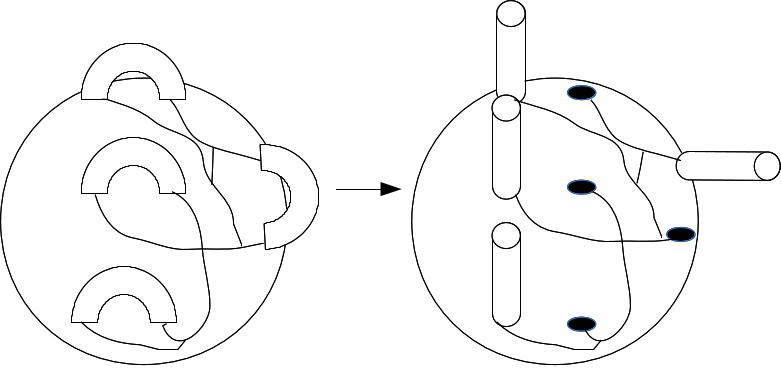
There is a vertex at the end of each pipe. From this vertex draw and edge to the vertx at the pase of the pipe.
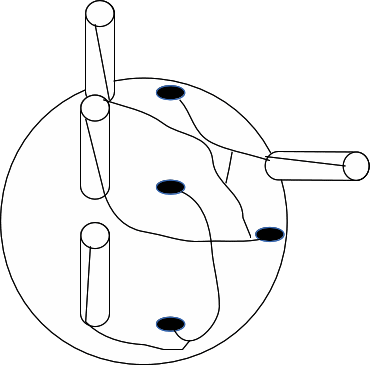
In order to close the surface turn the holes into faces. There are faces created at the end of each pipe and where the handle is detached from the sphere - a total of 2n extra faces. There are two edges created for each handle - one at each hole when the hole is created and replaced by a disc, and one from the base of the pipe to the top, and there are n vertices created - one for each hole repaced by a disc.
The new surface is homeomorphic to a sphere. Hence
![]()