Theorem
The following statements are equivalent:
-
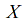 is compact.
is compact. -
For every family
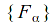 of closed subsets of
of closed subsets of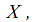
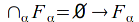 contains a finite subclass
contains a finite subclass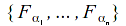 such that
such that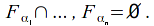
Proof
Suppose![]() then from De Morgans's Laws,
then from De Morgans's Laws,![]()
![]() is an open cover of
is an open cover of![]() because all the
because all the![]() are closed.
are closed.
Since![]() is compact a finite subcover
is compact a finite subcover![]() exists.
exists.
Again from De Morgans' Laws,![]()
Conversely, let![]() be an open cover of
be an open cover of![]() so that
so that![]() where each
where each![]() is open in
is open in![]()
From De Morgans' Laws,![]()
All the![]() are closed and have empty intersection. A subclass of
are closed and have empty intersection. A subclass of![]() exists such that
exists such that![]()
Again using De Morgan's Laws,![]() and
and![]() is compact.
is compact.