To prove Euler's equation![]() for a simple closed surface (homeomorphic to a sphere) start with a polygon drawn on the surface. Suppose the polygon has N vertices and hence N sides. The polygon has two faces - inside and outside the boundary so
for a simple closed surface (homeomorphic to a sphere) start with a polygon drawn on the surface. Suppose the polygon has N vertices and hence N sides. The polygon has two faces - inside and outside the boundary so
![]()
Suppose we now join two vertices by a polygonal curve - shown as red lines with blue vertices below.
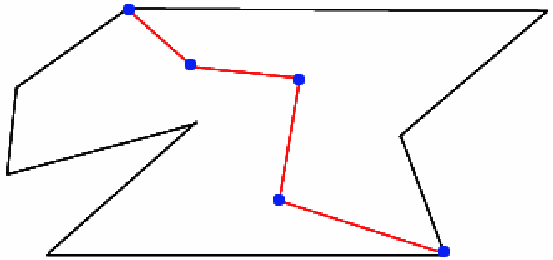
For a general curve of this type we add![]() new edges, n-1 new vertices qnd one new face. There are now
new edges, n-1 new vertices qnd one new face. There are now![]() faces,
faces,![]() edges and
edges and![]() vertices.
vertices.
![]()
If instead we do not draw the polygonal curves between existing vertices, then we will create an additional two edges in addition to the![]() edges along the polygonal curve we are adding, and two new vertices, where the new curve joins the existing polygon. In this case,
edges along the polygonal curve we are adding, and two new vertices, where the new curve joins the existing polygon. In this case,![]() and
and ![]()
![]()
This method can obviously be extended to any closed surface.