Theorem
If![]() is continuous then
is continuous then![]() exists such that
exists such that![]()
Proof
A continuous image of a connected set is connected since connectedness is preserved by continuity, so the image of the connected set![]() is
is![]() for
for![]() This is illustrated below.
This is illustrated below.
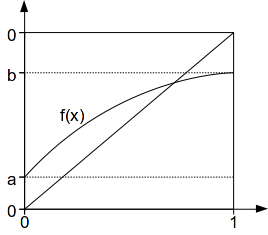
Hence the graph of![]() must intersect the diagonal from
must intersect the diagonal from![]() to
to![]() hence
hence![]() exists such that
exists such that![]()