Proof That a Discrete Topological Space With Two or More Points is Disconnected

Theorem

A spaceis said to be disconnected if the setcan be expressed as the union of at least two mutually exclusive, nonempty subsets of

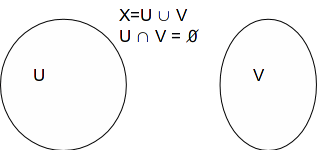
The setis connected if it is not disconnected.

Given a spacewith the discrete topology, takeand consider the sets

Both these sets are open andand

and (X,T) is disconnected.

Any set with the trivial topology is connected since the only nonempty open subset ofis itself.