Theorem
An open disc in the Euclidean plane setr^2 is path connected.
Proof
Let![]() and
and![]() be any two points of an open disc in
be any two points of an open disc in![]()
We can define a path from![]() to
to![]() as
as![]() for
for![]()
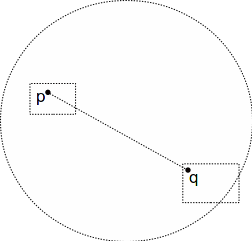
![]() is the line segment from
is the line segment from![]() to
to![]() contained completely in the unit disc hence the open disc is path connected in the plane.
contained completely in the unit disc hence the open disc is path connected in the plane.