Theorem
Let![]() be one to one continuous function
be one to one continuous function![]() from a compact space
from a compact space![]() into a Hausdorff space
into a Hausdorff space![]()
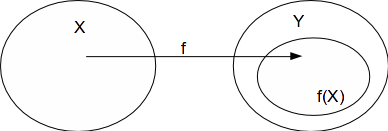
![]() is homeomorphic to
is homeomorphic to![]()
Proof
![]() is a continuous bijection, hence one to one and onto. Hence
is a continuous bijection, hence one to one and onto. Hence![]() exists and is well defined.
exists and is well defined.
![]() is continuous if, for every closed subset
is continuous if, for every closed subset![]() of
of![]()
![]() is a closed subset of
is a closed subset of![]()
Let![]() be a closed subset of a compact space, then
be a closed subset of a compact space, then![]() is compact. Since
is compact. Since![]() is continuous
is continuous![]() is a compact subset of
is a compact subset of![]()
![]() is Hausdorff, since it is a subspace of a Hausdorff space, hence
is Hausdorff, since it is a subspace of a Hausdorff space, hence![]() is closed and
is closed and![]() is continuous.
is continuous.
Hence![]() is a homeomorphism.
is a homeomorphism.