Theorem
If a topological space![]() is second countable it is separable.
is second countable it is separable.
Proof
Suppose![]() is a second countable space. Then there exists a countable base
is a second countable space. Then there exists a countable base![]() of
of![]() For each
For each![]() choose
choose![]() such that
such that![]()
The set![]() is countable. Let
is countable. Let![]() and let
and let![]() be an open set containing
be an open set containing![]() At least one set
At least one set![]() exists such that
exists such that![]()
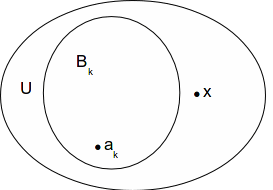
Since![]() and
and![]()
Hence![]() is an accumulation point of
is an accumulation point of![]() since every open set containing
since every open set containing![]() also contains a point of
also contains a point of![]() different from
different from![]()