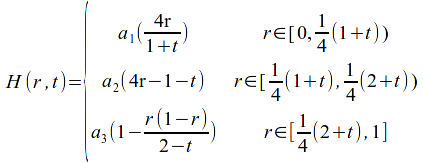Theorem
![]() is an equivalence relation on a set
is an equivalence relation on a set![]() for the set of loops with the same base point
for the set of loops with the same base point![]() with
with![]() if
if![]() is
is![]() loop in
loop in![]() homotopic to a loop
homotopic to a loop![]() and
and![]() and
and![]() have the same base point
have the same base point![]() The set of homotopy classes is then
The set of homotopy classes is then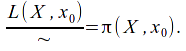
Associativity on the set of homotopy classes, written![]() is preserved, so that
is preserved, so that![]()
Proof
Let![]() be any three equivalence classes in
be any three equivalence classes in![]()
By definition,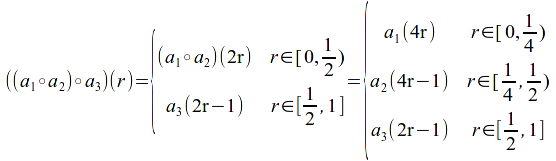
and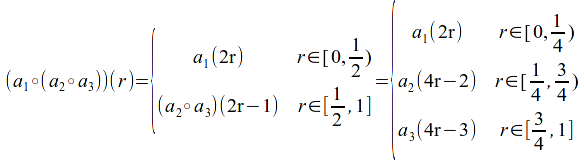
The homotopy between![]() and
and![]() is defined as
is defined as