Proof That a Union of Path Connected Subsets of a Space With Non Empty Intersection is Path Connected

Theorem

Letbe a class of non empty connected subsets ofwith non empty intersection so that

Thenis path connected.

Proof

LetPath connected subsets ofexist such that

The non empty intersectioncontains at least one point, say

Thenso there is a pathinfromtowithandso there is a pathinfromtowith

Define

by

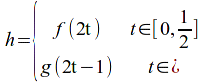
Thenis a path fromtoandis connected.