Theorem
Connectedness is a topological property. Equivalently, if
and
are topological spaces and
is continuous, then if
is (dis)connected then
is (dis)connected and vice versa.
Proof
Supposeandare topological spaces andis continuous. Suppose is connected and Y is not connected. Then there are open sets
such that
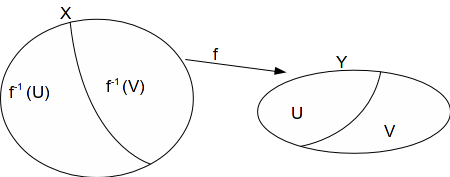
Since
is continuous,
are open sets in
Sinceis a bijection,
and
Henceis disconnected - a contradiction. Henceis connected.
The other implications are very similar.